Simulating the 2022 World Cup Knockout Stage
December 3, 2022

(World Cup trophy Photo by Rhett Lewis on Unsplash)
A few weeks ago I had grand plans to create a simulation model for the entire 2022 World Cup from the Group Stage through to the Final. However, a bout of strep throat and some travel over the Thanksgiving Break took some time away from my model-building efforts. So, instead of building a simulation model for the whole tournament (the Group Stage is over by the time this blog post is being written), I’ve developed a model for the Knockout Stage.
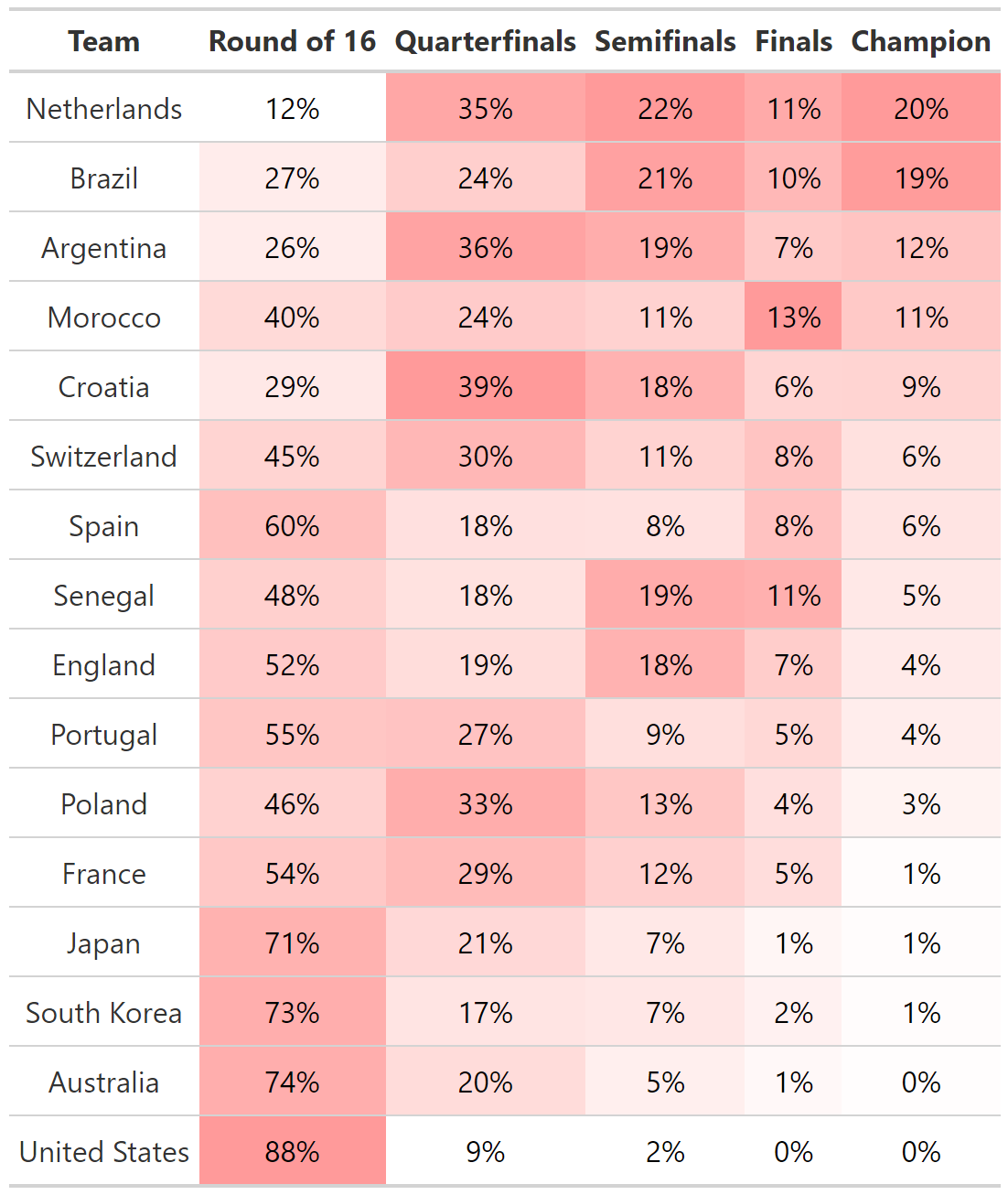
The World Cup begins with a Group Stage. Eight groups of four teams are formed and each team in a group plays the three other teams in their group. The top two teams from each group advance to the Knockout Stage. In the Knockout Stage, group winners are matched with group runners-up in the Round of 16. For example, the United States placed second in Group B. In the Knockout Stage they were matched against the Netherlands, the winner of Group A. The bracket (from Wikipedia) is shown below. Note that two of the Knockout Stage matches were completed before this blog post was published.
Data and Methodology
This work is inspired and motivated by work from Luke Benz @recspecs730 on Twitter and David Sheehan. The dataset for this work comes from Kaggle and includes match scores for matches from 1872 through the end of 2022 World Cup Group Stage. This dataset is updated regularly.
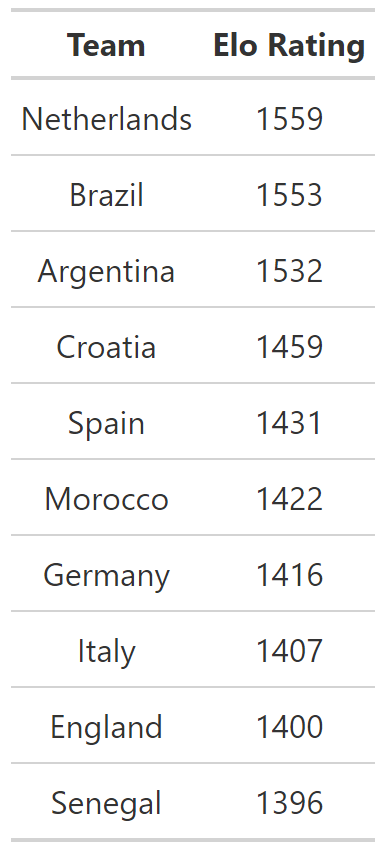
We start by using the match results from the Kaggle dataset to build an Elo ratings model. We’ll use the team Elo ratings as an overall measure of team strength. Elo models are nicely described on Wikipedia. To ensure that we have sufficient data to generate stabilized Elo ratings, we use match results from the beginning of qualification for the 2014 World Cup. We exclude any teams that played less than 25 matches over this time frame. This eliminates non-FIFA teams in the dataset (these teams tend to play infrequently). The top ten team’s in the final Elo ratings are shown below. For reference, the United States is ranked 26th.
Next we use Luke Benz’s methodology to build a Poisson regression model. Poisson regression can be used when the response variable is assumed to follow a Poisson distribution. The distribution of goals scored by a team in match can be reasonably assumed to be Poisson. For predictor variables we use: Team, Opponent, Match Location, Team Elo Rating, and Opponent Elo Rating. Each match in our dataset is weighted by the type of match played (similarly to how FIFA rankings are developed). For example, games that occur in the World Cup receive a higher weighting than friendly matches.
With our model built, we can (for any combination of teams) then estimate the mean number of goals scored by each team. This estimate serves as the Lambda value for the Poisson distribution. Let’s look at an example where the Netherlands and the United States play each other at a neutral site. The Poisson regression model predicts a Lambda value of 2.499 for the Netherlands and 0.513 for the United States. Using these Lambda values we can estimate the probabilities of scoring a particular number of goals. For the Netherlands, the probabilities of scoring 0 to 4 goals against the United States are shown in the table below.
| Goals | Probability |
|---|---|
| 0 | 0.082 |
| 1 | 0.205 |
| 2 | 0.257 |
| 3 | 0.214 |
| 4 | 0.134 |
For the United States against the Netherlands, the probabilities are:
| Goals | Probability |
|---|---|
| 0 | 0.384 |
| 1 | 0.367 |
| 2 | 0.176 |
| 3 | 0.056 |
| 4 | 0.013 |
From these probabilities, we can see that the most likely result is a 2-0 Netherlands win. The score from the actual match was 3-1 Netherlands. We can use this distribution of goals scored to simulate the match. For a given value of Lambda, R’s “rpois” function returns a random value from a Poisson distribution with a mean of Lambda. In the event of a tie in a Knockout Stage match, the match goes to Extra Time and then (if still tied) to a Penalty Kick Shootout. To simplify the model, we’ll assume that each team has a 50% chance of winning in the Extra Time/Penalty Kick Shootout.
Results
The Knockout Stage was simulated 1,000 times. Code for the simulation model is available on GitHub. The results of the simulation are provided in the table below. The table shows the percentage of the simulations in which the given team exited the tournament in the given round. The model holds the Netherlands in high regard, giving them the best chance (20%) to win the World Cup. Brazil comes in second at 19%. The United States sits in last place with only a 12% chance of defeating the Netherlands.